
Equation 1
Schwarzschild found the first exact solution to Einstein’s field equations of General Relativity in 1916. He found that 2Gm/r = c^2, the equation that describes a static black hole. This became known as the Exterior Schwarzschild Solution as it gives the metric of a black hole in the reference frame of an observer outside of it in ‘flat’ three-dimensional Euclidian space.
Soon afterwards, Schwarzschild derived an Interior solution for the metric inside a black hole. Unfortunately, he derived this metric in terms of the reference frame of an exterior observer, not of an interior observer.
This seems to have led Einstein to making his celebrated ‘greatest blunder’, the ad-hoc addition of a ‘cosmological constant’ to his equations to counteract the collapse predicted by the Interior Schwarzschild Solution when treating the universe as the inside of a black hole.
A gravitationally closed spacetime with three spatial dimensions must have the geometry of a Glome-type hypersphere with a metric of 2Gm/L = c^2 in the reference frame of any observer inside of it, where L shows the antipode distance.
(An observer inside the black hole of the universe can still use the exterior Schwarzschild solution when observing any of the smaller black holes within the universe from outside of them.)
The is confusion of observer reference frames has led to more than a century of confusion in cosmology and the development of the entirely erroneous model of LCDM Big Bang Cosmology.
Using the Interior Schwarzschild Metric in the reference frame of an Exterior observer has the effect of creating ‘Coordinate Singularities’ in the universe and inside of black holes.
Lines of longitude and latitude converge to form ‘Coordinate Singularities’ at the north and south poles of the Earth. However, no actual geographical singularity occurs at either place, the geography itself does not collapse to a tiny point or expand from a tiny point. Polar bears do not shrink to the size of mice if they stray close to the north pole.
The singularities that appear on globes of the Earth appear because we draw straight lines on their surfaces and the straight lines converge on the curved surface.
We now appreciate that the Earth has a curved surface, we do not live on a Flat Earth. It does however appear flat on a small local scale.
Nevertheless, lines of latitude and longitude still provide a grid of useful rectangles so long as we do not rely on this system too close to the poles.
Cosmologists mainly assume the universe has the flat geometry of ordinary Euclidian three-dimensional space that we see on the small local scale.
The universe does not have a flat Euclidian three-dimensional geometry on the cosmic scale. The mass inside the universe causes it to form a closed curved three-dimensional space under its own gravity. We live inside an awesomely vast black hole about thirteen billion light years across on the inside. A black hole of such a size does not have the sort of internal densities that characterise the smaller ones within it. A light dusting of galaxies spread over lots of nearly empty space can still provide gravitational closure at such a scale.
Cosmologists who persist in mapping the universe as flat will end up creating a Coordinate Singularity which looks like a Big Bang event in spacetime. This has no physical reality. The universe has the same curved geometry everywhere and at all points in time, rather like the surface of an ordinary sphere but in three dimensions.
Cosmologists mainly map or model the inside of black holes within the universe in terms of a Schwarzschild metric, but they speculatively map the internal metric in the reference frame of an external observer rather than in the reference frame of an internal observer of the metric. Thus, they wrongly conclude that a black hole must contain a spacetime singularity.
The Big Bang exists only as a Coordinate Singularity in the minds of theorists.
Beware of mistaking the map for the territory.
Because both the universe as a whole and the black holes within it consist of gravitationally closed spacetimes they have the curved geometry of Glome type Hyperspheres. These do not have real spacetime singularities but coordinate singularities will appear in predictions and calculations that mistakenly assume a flat geometry.
We do not inhabit a flat Earth. We do not inhabit a flat Universe either.
We inhabit a Hyperspherical Universe without Singularities.
How much spacetime does the universe contain? Conventional LCDM Big Bang Cosmology asserts that the observable universe has a radius of about 13.8 bnlyr, but that due to its apparent expansion since a hypothetical big bang it may now extend to perhaps 95 bnlyr and it may have the potential to expand into spacetime indefinitely.
Hypersphere Cosmology asserts that the entire universe consists of a finite but unbounded Hypersphere, closed in both space and time with an Antipode length of only13 bnlyr. This still makes it awesomely huge, but considerably smaller than the observable LCDM universe and certainly not even potentially spatially infinite. Such a Hypersphere will exist within a Black Hole with a radius equal to the Hypersphere’s Antipode length, as shown below.
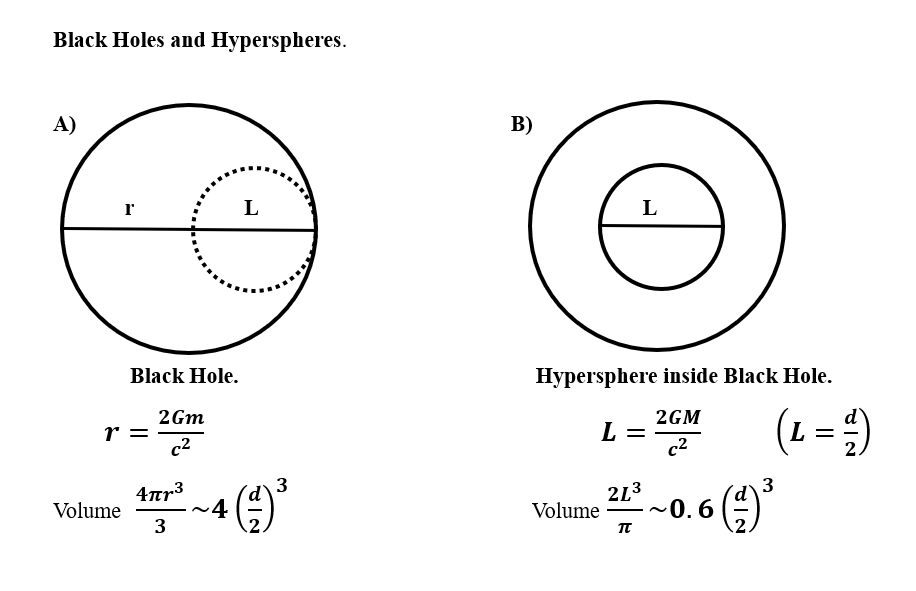
Physicists commonly assume that if matter collapses under its own gravity to form a black hole with a Schwarzschild radius of 2GM/c2 then it will continue to collapse until the matter forms a zero size singularity inside that Schwarzschild radius. The Penrose – Hawking Singularity Theorems assert this, but only on the basis that they cannot conceive of anything that would stop it.
Hypersphere Cosmology asserts that matter will cease to collapse within a black hole when all the matter has collapsed to half the Schwarzschild diameter because at this point a Hypersphere will form within the Black Hole. Such hyperspheres will have a rotational velocity of lightspeed and will resist further compression which would push their rotational velocity past lightspeed.
If the Schwarzschild radius r and the Hypersphere antipode length L both equal 2GM/c2, then L = r, or L = d/2. See A).
If we inhabit a universe that consists of the inside of a Black Hole and a Hypersphere has formed within it, then the optical horizon conventional cosmologists estimate to lie at ~13.4 bnlyr, and which Hypersphere Cosmology estimates to lie at almost exactly 13 bnlyr, represents the universe’s antipode distance not its radius.
If so, then the Hypersphere Cosmology universe has considerably less volume and a considerably higher density than conventional cosmology currently asserts. No surprise perhaps that the Hubble Deep Field contains so many galaxies.
Furthermore, a Black Hole of any mass within the universe should contain a Hypersphere.