Into the Darkness.

The last late Dragonfly of the season took to the air above the pond at Chateaux Chaos a week ago. She hovered around planting her eggs in the moss and weeds. In three years’ time her children will emerge having gorged themselves on the toadpoles in the depths.

As the evenings draw in, and the nights become chill and clear, it seems time to prepare poetry for the Samhain Eisteddfod, to invoke the Elder Gods, and to return again to cosmological questions.

Standard conventional Big Bang Cosmology depends on the idea of an expanding universe, and the fairly recently observed mismatch between the redshifts and the luminosities of type 1A supernovae has led to the further twist that the hypothesised expansion of the universe has apparently progressively speeded up during the last half of its expansion to date.

Despite the manifold problems with all versions of the Big Bang theory, and its general metaphysical distastefulness, it seems difficult to find papers on cosmology that do not automatically assume that we inhabit an expanding universe and which try to interpret all observational data accordingly.

However an interesting exception occurs here  http://arxiv.org/pdf/1002.0525v1.pdf

The ‘Angular Size’ of structures in the cosmos may give some indication of the geometry and topology of the universe in space and time. Many models based on expansion predict that structures at very great distances in space (and therefore time), should appear magnified because of the subsequent expansion.

Hypersphere Cosmology also predicts the magnification of very distant structures, but for a different reason. In Hypersphere Cosmology the small positive spacetime curvature of a non-expanding (vorticitation stabilised) cosmic hypersphere will exert a lensing effect which will not only magnify very distant structures but which will also diminish closer structures. This diminution of closer structures will create the optical illusion of a universe which appears to have undergone an accelerating expansion during the last half of its expansion to date, if observers wrongly assume that they look out over a gravitationally ‘flat’ universe.

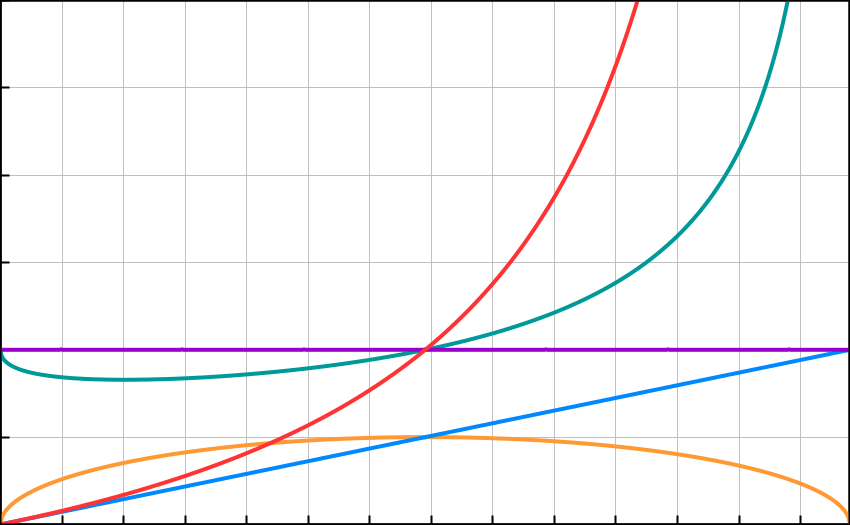
In the graph below the horizontal axis, (shown marked with 1 billion light year divisions) stretches from the observer at the origin to the limit of observation which corresponds to the hyperspherical antipode distance in Hypersphere Cosmology. We have used the figure of 13.8 billion light years here. The actual distance may differ slightly from this; we await a more precise measurement of the Anderson deceleration or the undistorted Hubble distance.

(GM/L^2 = A, where G = Gravitational constant, M = Mass of universe, L = Antipode distance which corresponds to Hubble distance, A = Anderson deceleration which corresponds to the spacetime curvature.)

The vertical axis for a number of factors runs from zero to three, marked in divisions of 0.5 with the unity line highlighted in purple for clarity.

The red line shows redshift Z, where Z = (c/(c-(dA)^0.5)-1 where d = astronomical distance.

Note that a redshift of 1 at about 7 billion light years denotes the halfway point to the antipode distance. Redshift climbs exponentially towards infinity at the antipode; observations become increasingly difficult up to redshift 10 and then virtually impossible beyond.

The yellow line represents schematically the hyperspherical geodesic from the observer to the observer’s antipode; the curved path that light actually takes in the cosmic hypersphere.

The blue line represents schematically the observer’s assumed sight line for flat space.

The green line represents schematically the difference between the actual and the assumed sight line, and thus the degree of Hyperspherical Lensing L_H, that light becomes subject to at various distances. Note that in this revised version of the model, the line has the inverse configuration to previous models on this site and the equation governing it has the form

L_H  = 1/(1+((d-d^2)^0.5))-d) where here, d = astronomical distance/antipode distance.

The negative lensing at distances below 7 billion light years explains the anomalously low luminosity of type 1A supernovae without recourse to the hypothesis of an accelerating expansion driven by some mysterious dark energy.

The positive lensing at distances greater than 7 billion light years explains the increase in angular size of very distant structures without recourse to the hypothesis of an expanding universe at all.