Arcanorium CollegeCollege News and Views
Pete Carroll
Equation 12

Equation 12
The Bekenstein-Hawking conjecture arose to explain the behaviour of entropy in a black hole.
https://en.wikipedia.org/wiki/Black_hole_thermodynamics#Overview
It asserts that the entropy does not disappear but becomes preserved by an increase in the surface area of the hole in Planck units if matter falls in.
As the universe itself consists of a black hole in Hypersphere Cosmology then its surface area should represent the total amount of entropy that it contains.
Using the square of the antipode length L over the Planck area to approximate the entropy we obtain an entropy of the order of e120.
If the entropy of a system equates to its information content, then e120 bits of information must suffice for the e180 Planck volumes within the universe.
This implies only one bit of information per e60 Planck volumes or one for each e20 Planck length.
The universe thus has insufficient information to specify anything below this level of its effective pixilation.
See equations 13,14, and 15 for the consequences of this.
None of this supports the Holographic Universe hypothesis. The surface area defines the entropy/information content, but the information is not ‘encoded’ on the surface.
We can obtain a similar result by using the ratios of 3D surface hyper-areas.
The Conservation of Entropy.
Hypersphere Cosmology asserts that the overall entropy of the universe remains constant.
The second law of thermodynamics states that the entropy of a closed system must either increase or remain constant, it can never decrease.
The sky is cold, the stars are hot, plainly the observable entropy remains fairly low, but many of the processes going on around us appear to increase entropy
Now as the limits of observation represent a temporal horizon rather than a temporal boundary, the matter and energy within it has had unbounded time during which it has plainly not achieved thermodynamic equilibrium and maximum entropy.
Thus the universe must have some ongoing processes which increase entropy and some which do the opposite, and between them maintain an overall constant entropy. Gravitation itself may supply the main entropy reversing mechanism.
The principle of never decreasing entropy, the second law of thermodynamics, grew out of the age of steam and observations of the flow of heat in gasses. It takes no account of the attractions between particles. Observe some gas with an uneven distribution of heat or pressure and it will soon homogenise or dissipate. However, a really vast amount of gas will compress itself and ignite as a star. I submit that it be considered as an entropy reversing effect.
If gravity worked repulsively it would fit the simple view of entropy nicely, matter and energy would dissipate. Interestingly the sign of G is formally negative, although we can usually ignore that, but in a sense, gravity reverses the (entropic) arrow of time.
'Entropy increases with time because we measure time in the direction in which entropy increases' - Stephen Hawking.
Equation 10 shows that black holes within the universe will not persist indefinitely.
Neutrons build up as stars burn and create heavier elements but heavier elements breakdown into neutron plasma inside neutron stars which eventually explode. Free neutrons in space decay back into hydrogen.
The recently discovered Giant Gas Halos around nearby galaxies suggest that all galaxies probably have these difficult to observe halos. Such halos, which also contain heavy element dust from exploded stars, may well act as the recycling yards for the stellar parts of the galaxies.
We have no means of determining the ages of black holes and some structures within the universe seem to have an age very close to, or in excess of, the temporal horizon.
It does not seem unlikely that the closed spacetime of the Hyperspherical Universe can maintain a constant leel of entropy.
Equation 13

Equation 13
The universe has an information deficit in the sense that it has only one bit of information/entropy for every e20 Planck lengths and this represents the universe’s pixilation or ‘grain size’. Equations 14 and 15 show what this means for quantum particles.
The pixilation level also has the effect of raising the effective Heisenberg uncertainty/indeterminacy level of the universe by twenty orders of magnitude. This does not make the universe excessively Chaotic in principle, but it does make it about as Chaotic as it appears in practice.
Equation 14

Equation 14
The universe has an information deficit in the sense that it has only one bit of information/entropy for every e20 Planck lengths and this represents the universe’s pixilation or ‘grain size’. In practise we do not observe anything physically real at LESS than twenty orders of magnitude Above the Planck Length or Above the Planck Time.
See below: -
Equation 15
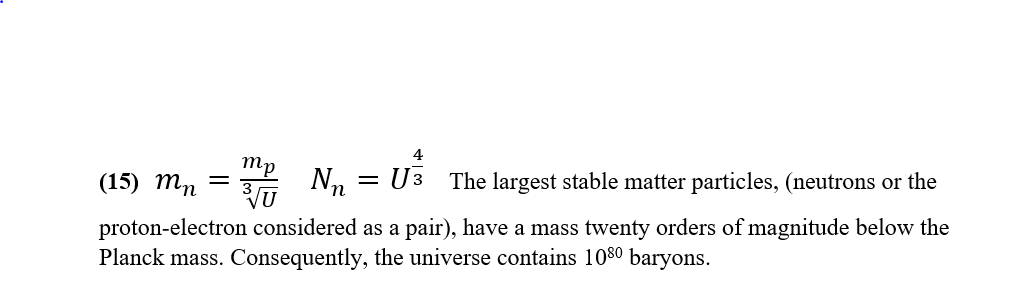
Equation 15
It may seem odd that whilst the ‘enhanced’ Planck length and Planck time set a lower limit for quantum particles, (see equation 14) whilst a similarly ‘reduced’ Planck mass sets an upper limit for the size of stable quanta.
However, the wavelength of a quantum is inversely proportional to its mass, heavier quanta have smaller not larger wavelengths.
Stable quanta cannot have a mass in excess of e-20 Planck mass or their wavelengths would fall below the pixilation level of the universe.
See below: -
Equation 16
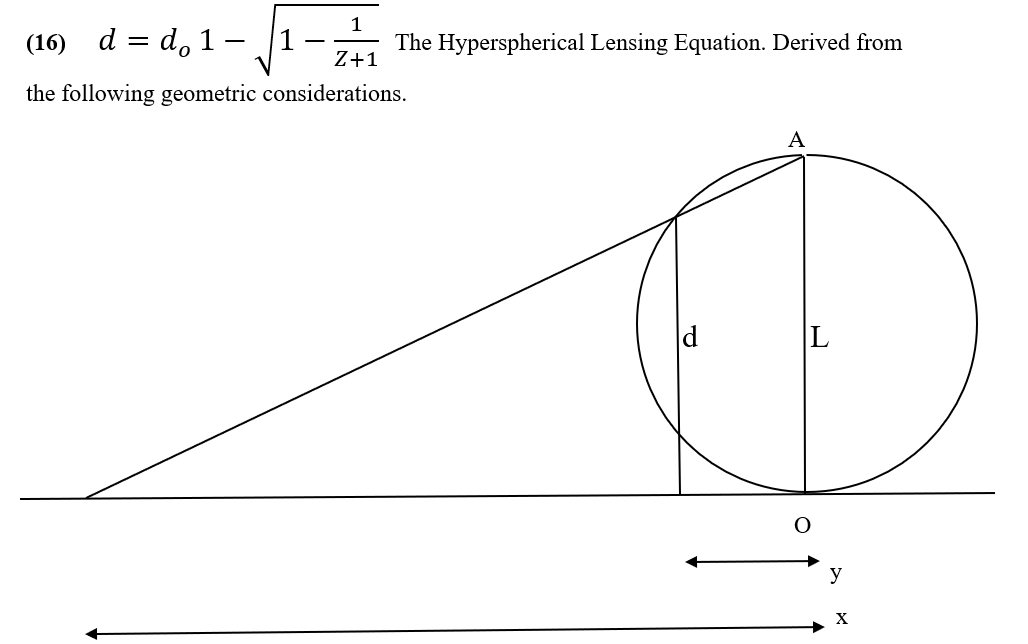

Equation 16
A stereographic projection can show the effect of projecting an n-sphere into an n-dimensional space.
For the purposes of Hypersphere Cosmology, we require a projection of a 3-sphere into three-dimensional space as observers will measure light as having travelled to them in ‘straight’ lines.
The diagram shown projects a 1-sphere (a circle) into a 1-space (a line), but this will suffice as we only need to know the distortion of distance.
Imagine first the projection of a 2-sphere (say a globe) into a 2-space (a flat surface). Imagine that we construct a wire frame globe with lines of latitude and longitude made of wires. If we place the globe south pole down on a sheet of paper and then place a lightbulb just inside the smallest ring of latitude around the north pole. The light will throw a shadow of the latitude wires of the globe onto the paper. The latitude rings close to the south pole will appear as circles close to the south pole on the paper, but latitude rings further from the south pole will start to appear exponentially larger and further away from the south pole on the paper. In principle, the shadow from latitudes very close to the north pole will go off the edges of a sheet of paper of any size.
Now a Glome-type hypersphere has the property that its circumference equals twice its antipode length L, so the distance d equals the distance around the circumference from the observer at the origin O at which we seek to determine the projection.
Such stereographic projections project a circle into an ever more widely spaced series of points on a line. A sphere becomes a series of ever more widely spaced concentric circles on a plane, a Glome hypersphere becomes an ever more widely spaced series of concentric 3D spheres. The equation shows the same distance relationship in all the various dimensional scenarios.
By expressing distance d over antipode length L and converting to redshift Z using the Redshift-Distance Equation we can relate the distance distortion from apparent to actual distance caused by lensing directly to redshift.
This shows that the universe does not undergo an accelerating expansion and does not need Dark Energy. It also allows a precise determination of the antipode length of the universe by Equation 17.
Equation 17

Equation 17
The Redshift-Distance and the Lensing equations 6 and 16 together yield a derivation for the Antipode length L for the universe.
This derivation depends only on measured redshifts and measured apparent distances derived from measured apparent magnitudes.
As shown in the extensive calculations here: -
A value of L close to 1.23 e metres emerges in every case, within the limits of observational inaccuracies in apparent magnitude observations. This corresponds to 13 billion light years.
The substitution of this value for L into equation 1 gives the exact value of the mass of the universe M at 8 e52 kilograms, eighty octillion metric tonnes.
The substitution of this value for L into equation 2 gives the exact value of A the spacetime curvature of the universe expressed as an acceleration of 7.317 e-10 metres per second squared.
The substitution of this value for L into equation 5 gives the exact angular velocity of megastructures around the universe as 0.005 arcseconds per century on the basis that they rotate around the great circles of a Hopf Fibration of the hypersphere with a circumference of twice the antipode length L.
Feblog 2021
Feblog 2021
Covid
The Memsahib and I have just had our Covid 19 jabs. Trivial side effects passed within a day.
Astra-Zeneca, just what we wanted, thanks very much.
Thank all the gods that we have such brilliant scientists on this sceptred isle and that we escaped from the damnable EU.
Logically and Ethically, anyone who refuses the civic duty of taking the jab without good medical reason should also refuse hospital treatment for covid if they need it - and take their chances at home. The loss of anti-vaxers can only improve the collective intelligence of humanity.
Alternative Physics
This blog comes a bit late because of a ferocious battle in progress. I exposed Hypersphere Cosmology to a panel of anonymous experts on an internet forum, see the ‘Against the Mainstream’ threads https://forum.cosmoquest.org/ A Hyperspherical Universe without Singularities.
It has been algebra at dawn with references flying like bullets for weeks. Its meant waking in the middle of the night to scribble down half formed equations for the next morning’s hostilities.
So far Hypersphere Cosmology https://www.specularium.org/hypersphere-cosmology
has resisted falsification and strengthened its defences, see the upgraded Equation 6 and this new paper refuting the dark matter hypothesis: -
https://www.specularium.org/component/k2/item/290-galactic-rotation-curves
Politics
The sky has not fallen in since Brexit, despite the additional problems of covid the UK has survived, and despite also the spiteful interpretation of non-tariff barriers by the damn EU.
The EU itself has made an almighty pig’s ear of its vaccination program. If the EU functioned as a democracy, heads would have already rolled. But no, it functions as a Crony-Synarchy.
The Scottish National Party has predictably tried to exploit the covid crisis, but why will no SNP politician state clearly what Scottish Independence mean in terms of currency, central bank, national debt, border control, and the vast subsidy it currently receives from the UK? I fear Lowland Clearances – large numbers of economic migrants fleeing south to escape an imploding Scottish Economy.
The Scottish voice counts for quite a lot in the government of the UK, in the government of the EU it will count for very little indeed.
I love Scotland and I love Tartan Romanticism - althought that's not a credible politico-economic policy, just an invention of Sir Walter Scott.
The Scottish Enlightenment began with The Act of Union, long may it continue..
The Auld Alliance (with France) never served Scotland well.
New Year 2021
Pandemic
Chinese bats now seem to have killed more Brits than the Luftwaffe, or indeed the annual toll of WW2 did. Nevertheless, we have a home-grown vaccine that may well sort this out by the summer here and in the entire world thereafter. I hope that we do not punish the government at the next election. This pandemic represents a disease of progress and civilisation – our fault for exploiting wild animals and encouraging mass travel around the globe. Authoritarian regimes have had much lower casualties, but freedom has a price, better Dead than Yellow or Kraut. The Labour opposition here has whined and bleated, failed to come up with policy alternatives, and grudgingly agreed to the government’s tactics. Let us thank all the gods we did not have Comrade Jeremy Corbyn in charge during this crisis.
Politics
Culture War or Class War?
Here in the UK, we have an irritating amount of overspill from the so-called ‘Culture Wars’ allegedly wracking the fabric of American society.
Wokeism, Anti-Colonialism, BLM, Cancelism, and Minority Sexuality advocacy seem to have coalesced into a single liberal virtue signalling package against which an equally polarised backlash has formed to promote White Supremacy, Anti-Globalisation, Nationalism, and Conspiracy theories.
What underlies this Polarisation? - The Economy.
For the last several decades the professional and managerial classes in the USA, and to some extent the UK, have screwed the lower middle and working classes through globalisation. The wages of the poorer in rich countries have stagnated or declined in real terms as manufacturing has become outsourced to the developing world or insourced to cheaper imported labour. Meanwhile the managerial and professional classes have profited from cheaper goods and services and capital invested overseas.
This becomes all too clear when you examine ‘The Elephant Graph’. -
https://www.ejiltalk.org/being-charged-by-an-elephant-a-story-of-globalization-and-inequality/
The rich in rich countries often opine that they have helped to uplift many parts of the developing world and that this would lead them to adopt western style values and democracy. The later has singularly failed to materialise. The rich in rich countries have merely succeeded in shifting wealth to themselves, and from the poor in their own countries to the rich in poor countries.
All the issues which have become polarised into the so called ‘culture wars’ revolve around the concerns of the poor in rich countries.
The American dream of a working-class family with their own home and car and with one parent as homemaker now seems a rarity or a forgotten fantasy for many. I has also become exceedingly difficult to achieve in the UK.
QAnon’s seemingly mad ideas about a conspiracy of ‘Satanic Paedophiles’ actually makes a certain amount of metaphorical sense if interpreted as a conspiracy of ‘Greedy Capitalists Denying Poor Children a Future’.
Yet for all sorts of historical reasons America can never admit that it has a Class War, so a Culture War stands in as a proxy for it. Socialism comes close to blasphemy in the land of the free, and in the land of the free, many choose to regard poverty as self-inflicted despite the glaring inequalities of opportunity.
The American democratic party, rather like the British Labour party, now seems dominated by Rich Liberals, and both ignore the lower orders whose mores and habits they despise.
Liberalism sets great store in an offensive against the side effects of relative poverty rather than its cause. Thus, it campaigns for any imaginable minority grievance rather than address the underlying economic factors which give rise to them.
Many Americans voted for Trump in the hope that he would do something about the American response to Globalisation. He seemed a strange choice but nobody else from the American elite dared to put themselves to the task, and America elects only from what it considers its elite. Trump may or may not now disappear, but the underlying issue will not, particularly under the pretence that it remains a Culture War.
Do not expect a revolution. Revolutions the world over, only tend to succeed under middle-class leadership.
Many British voted for Brexit in the hope it would allow us to deal with globalisation on terms of our own choosing. Our Conservative government at last talks openly about levelling up the economies of our poorer areas and classes. I live in hope.
Esoterics
The main part of this blog consists of an extensive email interview that Mr Ian Blumberg-Enge requested I give. This took place over the last week, because of its substantial size I have placed it here: -
https://www.specularium.org/wizardry/item/308-interview-january-2021
Interview January 2021
An email interview between Ian Blumberg-Enge (in bold type) and Peter J Carroll.
Awesome! Maybe we could start with your current project, an alternative theory to the big bang? Is it possible to give a basic description? What is wrong with or missing from the big bang? How did you get into this project?
Back in the 1990s a flurry of popular science books came out on the Big Bang theory. At the time I had been conducting a series of seminars and tours about Chaos Magic and founding an international chaos magic order – The IOT. Several participants suggested parallels between the idea of a big bang explosive beginning to the universe and the idea of a primal chaotic creativity underling the mind and the universe, and the ancient Greek idea of the universe arising from Chaos.
At an Austrian Castle we conducted a mass dreamwork scrying experiment following a ritual to send an entity back to the time of the big bang to have a look at it.
Strangely, most participants reported that the universe then looked broadly the same as it does now.
This sent me on a twenty-year quest to resolve the issue. I had a science degree but in Chemistry rather than Physics. Nevertheless, I plunged into the study of cosmology to discover in detail just why so many physicists supported the Big Bang theory. This quest took me through thousands of scientific papers and books and entailed a substantial upgrade to my maths skills.
What I found rather shocked me and goaded me to further efforts. The Big Bang theory had become concocted in defiance of scientific method; it began with an experimental assumption about the redshift of distant galaxies and all subsequent observations have become interpreted in terms of that assumption, no matter how awkward the fit. Later observations that seemed to contradict the initial assumption did not provoke a significant questioning of it, instead they became explained away by inventing vast imaginary cosmic phenomena like so-called dark matter and dark energy. In any other field of science, you could not get away with this, much less get Nobel Prizes for it.
I found it increasingly irritating to find so many cosmologists and popularisers asserting that ‘We KNOW that the universe is expanding’. I also found the Big Bang theory increasingly unsatisfactory in metaphysical terms for it implied a creation event and an eventual apocalypse which gave some comfort to those with a monotheist religious outlook. (One of the main initial architects of the theory - Georges Lemaitre, also had a career as a catholic priest).
After a great deal of struggle and with some assistance from rebel astronomers and mathematicians and invocations for inspiration from extra-terrestrial entities, (these may only exist in my imagination, I often try magic when I have exhausted the possibilities of common sense), a coherent alternative to the Big Bang theory emerged.
I will not go into the details here, the exposition takes an hour or more, but the Hypersphere Cosmology model does fit all the observational data we have to date yet without having to postulate imaginary and unobservable phlogiston like phenomena such as spacetime singularities, inflation fields, dark matter, or dark energy.
The essentials of the new model appear here https://www.specularium.org/hypersphere-cosmology
In short, in the Hypersphere model we have a universe finite but unbounded in both space and time. From the perspective of observers within it (such as us) it has a definite size and a temporal horizon, but we cannot get out of it or to the end of it, so it will appear to go on forever. The final piece of the model came together with a re-analysis of Perlmutter’s data. Conventionally this became interpreted as an accelerating expansion and which led to the idea of a mysterious dark energy driving it. The Hypersphere interpretation shows that the spacetime curvature of the entire cosmos distorts distances like a giant lens and that we see it in stereographic projection. This makes the universe look potentially infinite, but the hypersphere model shows that after a ‘mere’ thirteen billion light years journey you would start moving back towards where you set off from. Something analogous applies to time as well, but do not expect the universe to do exactly the same things each ‘time around’.
Anyway, having sorted that to my metaphysical, mathematical, and scientific satisfaction, I have now turned to the question of the quanta that seemingly underlie all the matter and energy in the cosmos. The current official model, Quantum Field Theory looks as much of an ad hoc mess as does the official Standard Big Bang Cosmological Model. This may take a while to say the least.
My motivation for these quests to see beyond the current official models has two roots. Firstly, I seek to find a natural physical explanation for magical phenomena. My books so far have detailed magical philosophy and practise – basically what to do to increase the probability of making magic work. As to precisely how it works, I would like to know. I suspect it involves something on the quantum level. Initially I began looking there but the question of the nature of time and space and the dynamics of the cosmos seemed to side-track me into cosmology. However, the hypersphere geometry that emerged from the cosmology now appears to have much to offer in explicating the quantum realm. As above so below.
Secondly, in the grand scheme of things, evolution’s gamble in experimenting with humans will only pay off long term if we manage to work out how to make starships and spread the terrestrial biota to other star systems. Contemporary official theories of physics say we cannot possibly do this. I would like to change that.
Nothing Has Ultimate Truth, Anything Remains Possible.
Interroga Omnia – Question all things.
Was this mass dreamwork in Austria the first time you used magic for scientific ends, or do you not see a worthwhile reason for distinguishing the two at all?
I consider myself a Natural Philosopher of the old style like Newton, prepared to look at both science and magic. Scientific and magical thinking complement each other in my view.
Sending an entity back in time seems like a clever yet straight forward application of a magical technique for a scientific end, are there other magical techniques you like for scientific work?
I frequently invoke the goddess Apophenia for scientific inspiration. Her ontological status remains a matter of debate. Imaginary friend? Part of my own subconscious? Grecian style goddess with a mind the size of a planet? As a Chaoist I have a situational belief structure.
Are there current or past models, like orgone, that you like for quantum phenomena?
Many mutually contradictory schemes of esoteric bodily energy exist. They do however all have one thing in common – the projection of attention and intent into the body.
I find the Transactional Interpretation the most interesting model of quantum phenomena, it says that time goes in both directions simultaneously, and it appears to have considerable explanatory power in magic.
In order for your new cosmological model and your coming quantum one to help get us to the stars do they need to be adopted by mainstream science,
I keep requesting that the scientific community falsifies the Hypersphere Cosmology. So far nobody has. Hopefully, an insider or group of insiders will either show a mistake in it or run with it. Before we go to the stars, we need a good map.
…..and does the fact that you used magic to help formulate them hurt that goal?
Well. I made a successful commercial business without ever having a haircut or a suit. I think this persuaded my bankers, suppliers, and customers that I has sufficient confidence in my schemes. I hope that wearing my pointy hat openly will attract scientific attack and force the issue.
Like you said the big bang can be seen as a monotheistic interpretation, how much of that sort of thing is there in modern physics do you think?
In the west we inhabit a post-monotheist culture. Einstein famously refused to believe that god plays dice (quantum indeterminacy). The debate about causality vs a-causality rages to this day. Causality implies some form of initial cause, a-causality or retro-causality does not. The quest for a unified theory of all forces perhaps partly derives from a monotheist idea of unity.
And do magical experiments lend themselves more to either quantum or cosmic phenomena more?
That all depends on the experiment. Some of us like to use ‘Aliens’ as sources of power and inspiration, some do this metaphorically, some invest deeper belief in them, cosmological theories may well have some influence on our choices about what to expect of ‘Aliens’.
I always recommend taking a ‘quantum’ view of results magic because it seems to work by probability modification rather than by direct causality. The quantum view leads to the principle of ‘enchant long and divine short’, and this seems good practical advice.
![]()
The natural philosopher comparison feels right on, but you seem to have a better sense of humour about your pointy hat than Newton did. Do you own a real point hat?
I currently have two black pointed hats, a specially made formal serious one over a foot high with an embroidered chaostar on it. I only use this when doing something important in full ritual/ceremonial magic. For everyday wear I have an ordinary black hat with the top pushed up to a point and the brim flattened under hot water. This makes a distinctive though not wildly ostentatious hat. Biologists have noticed that if all members of a species look virtually identical it usually indicates that the species lies under intense selection pressure. The same seems to apply to human professions – look at all those suits in politics and business. I prefer to present myself as mildly contemptuous of selection pressures.
Newton seemed a very dour and antisocial type, fanatically devoted to the quest of knowledge and ideas, he also developed his manual skills and built himself the first reflecting telescope. I perhaps have a little of that, but I do have a small social circle and a wife and family. Fortunately, my wife reads a lot, leaving me time for research.
Do you think the current state of academia and information technology makes your job easier than in Newtons day or harder?
Information technology makes it possible to instantly obtain a stupendous cornucopia of up to date and historical scientific thought and data. It also makes it easy to find people you will probably never meet face to face, to discuss ideas with. Electronic calculations can reduce data crunching to the work of a moment rather than weeks on paper.
On the downside, information technology does seem to lead to a scientific herd mentality where everyone in the official herd comes under pressure to accept the same theories and academics tend to become the policemen of the intellect. Academics within the fold take a risk with their careers by even acknowledging contributions from without. Some of the more dubious assertions of conventional theories tend to become defended with almost religious fervour.
The Transactional interpretation, with time moving in both directions, fits within the Hypersphere model?
The Transactional Interpretation remains an unfalsified minority view of what goes on at the quantum level. Basically, it says that interactions consist of closed loops of waves going both forwards and backwards in time. It provides a way of visualising what actually happens in the otherwise bizarre and inexplicable double slit experiment, the apparent wave/particle duality, and in the seemingly impossible but measurable phenomenon of quantum entanglement. I hope to show that all those events we commonly regard as ‘particles’ consist of spin-waves of varied dimensionality that often extend in some sense right around the entire hyperspherical universe.
Does the Hypersphere model take a position on causality or imply some initial creative force other than refuting the big bang's constant expansion?
I seriously doubt that any big bang ever occurred. I suspect that the universe will appear broadly the same to any observer anywhere and any-when within it. The big bang theory does not tell us how the universe came into existence, it merely claims that a long time ago the whole thing occupied almost zero volume and had near infinite density and that our theories give us no clue as to how such a state arose.
Monotheist thinking suggests that Non-Existence somehow precedes or has a more fundamental reality than Existence. I do not buy that. Existence seems more fundamental to me. Something always exists and existence means continual change. Ultimately everything causes everything else across immense loops of closed space and time.
Scientifically speaking does the task of creating quantum models prove more difficult than cosmic ones? you don't need a super collider or something? What about accessing the proper data for one vs the other?
As most data from astronomical and particle observatories has no military or economic value it tends to become made available quite quickly in order to win prestigious prizes.
If I could do two experiments, I would do these two as a priority: -
Do a re-run of a deep space probe mission with high-precision telemetry to rigorously test the Pioneer Anomaly again.
Test the hypothesis that the so-called Higgs Boson consists merely of a ZZ Di-boson resonance.
Are you having to learn new maths?
I suspect and hope that the secrets of the universe remain comprehensible in terms of fairly simple algebra and geometry and that where we have ended up with descriptions that use exceedingly baroque and abstract mathematics we have not yet penetrated to the fundamentals.
This has become a serious problem in quantum matters. Current standard Quantum Field Theory consists of a mass of abstract mathematical operations and concepts that can partially model some of what the quanta seem to do. However, these bits of mathematics do not really translate into algebra or words or into geometry or images. As the great quantum physicist Richard Feynman quipped - ‘Nobody understands quantum physics’.
Wouldn't any new quantum model have implications for computing and energy?
Perhaps. Most would admit that the current official theory remains incomplete, if we manage to complete it further, we may find some existing parts erroneous. Presently we have dozens of competing interpretations of what the strange data and the mathematics used to describe them actually mean, perhaps some breakthrough here will lead to new testable predictions and new technology.
Why go to space? environmental disaster, it looks cool out there, DNA coding?
Hypersphere Cosmology asserts that for us as a species the universe will effectively persist indefinitely, and that we could do so as well. Thus, we need to look after the environment of this planet for as long as possible until astronomical events render it uninhabitable, and well before that we need to work out how to make starships – this will require something beyond our current physics. Presently we have economic systems that depend on growth of both population and consumption. This planet cannot support even the current human population and its consumption in the medium term, let alone in the long term.
I shudder to think what mistakes humanity will make when it starts re-writing its own genetics. A planet full of seven-foot-tall beautiful immortal super athletes all with an IQ of 200 might have poorer survival prospects than a planet full of three-foot-high vegetarians of mixed and eccentric abilities.
How did you get into ceremonial magic?
For me it began as a discipline for carrying out results-based magic in a formal way so that I paid minute attention to what I did, and nothing got left out. Later when I did stuff on my own, I tended to simplify the procedures to what seemed essential for me. Later still when I started setting up groups for collective conjurations, I found the ritual structure useful for coordinating and synchronising everyone’s efforts. However, by then I had simplified a lot of the traditional rituals to emphasise the effective important bits.
Was chaos magic created out of a need for a better working model?
Yes indeed, a lot of the old systems remained full of unnecessary beliefs and faux historical mythology. Magic continually reinvents itself and then pretends to an ancient hidden knowledge. You only really need intent and imagination and a few techniques for putting the mind into an extremely excited or a very quiescent state. You can dress it up with any beliefs or symbols that appeal.
Do you think it was important that you created a working model for tuning and hacking your inner space before moving onto modelling the cosmos?
Magic did wonders for my imagination and for my arrogance. The practise of stilling the mind and the imagination has the peculiar effect of making it work much more powerfully afterwards. Identifying myself as a wizard somehow obliged and inspired me to attempt extraordinary things.
Are the theatrical aspects of ritual magic (Austrian castles and pointy hats) as important after decades of ceremonial work?
The high years of large magical orders and mass interest in hardcore occult activities seem to have passed for various cultural reasons. So much occultism now consists of individuals working alone and communicating mainly online. Nevertheless, I still keep my hand in with the local Druid Grove once a month, we still use robes, staffs, candles, and circles.
For some historical perspective when were those high years and what did they look like? how many people at a large ritual and how often was that stuff happening? you were traveling the world giving classes and workshops also?
For me, the peak years seemed to run from 1985-95. At the castle seminars we had about 40 participants mainly drawn from the professional classes at the annual event for about 5 years running. I went to the USA 3 times to give lectures in esoteric bookshops. We had some events in London and a dozen or so temples that met in various cities around the world.
Long term you could say that your dreamwork in that Austrian castle in the 90's sort of didnt culminate until you finished your cosmological model and its impact still hasn't been fully realized. Are there still spells from those high years working themselves out on us all?
Some spells take ages; thus, we should always try to ‘Enchant Long’. In my earliest book I put a spell to ‘Obtain the Necronomicon’, a quarter of a century later I obtained one somehow out of the aether or my subconscious or with extra-terrestrial assistance. It seems to do the trick.
Has anything been lost do you think in that shift away from communal magic or is this an evolution or maybe just a lull? I don’t remember whose idea it was, but I think Wilson introduced me to the idea that it takes a generation for new information to integrate itself into a culture. I like to think that is what is currently happening to chaos magic and all the sort of open-source spiritual science from that era.
Often when I look at any modern book of magic today, I think well, we are nearly all Chaos Magicians now. Deep down I suspect that most neo-pagans (with perhaps a few American exceptions) believe the gods and goddesses exist as thought forms of our own creation and that in magical evocation you basically create ‘spirits’ as servitors, but they remain no less useful for that, in fact it makes them more useful and versatile.
Unfortunately, the internet gradually brought with it what I call ‘Internet-itis’ - a huge reduction in attention spans, a relentless need for continual novelty, and an increasing reluctance to put in sustained work. Plus, in an increasingly noisy medium the short shout has tended to replace proper debate and genuine exchange of ideas.
Wikipedia says Robert Anton Wilson invited you to teach at the maybe logic academy? what did you teach there, was it a physical location?
When Wilson got old and sick his friends opened an online academy that offered courses to raise money for his care. They invited me and quite a few others as tutors. I gave three or four courses of about eight weeks each, two in basic chaos magic and one on chaos magic in business. After it wound down, at the encouragement of participants I opened Arcanorium College online and carried on doing something similar for another near decade, until it began to suffer from internet-itis.
Did you know Wilson personally?
I spent two evenings with him at his place near LA when I did lectures over there. I found him very agreeable company and he had a mind like jet engine, voraciously sucking in ideas and mixing them with the fuel of his enthusiasm and blasting them out in accelerated form, though I often wondered if he lost track of them afterwards………
What did you study at university?
Officially mainly Chemistry with some Biology. However, I rapidly became bored with a chemistry that merely resumed what we had done in school but in excruciating detail, so I spent most of my time and energy studying esoteric and magical matters. In those days many of the core texts of western magic appeared in bookshops for the first time. I settled for a minimum pass at chemistry and an unofficial major in magic.
Wikipedia also says you taught in India and the Himalayas, what did you teach there? Did that experience influence your magic studies?
No, I spent many months studying English language works about Tibetan esoterics in the Tibetan Library at Dharamsala/McCleod Ganj. Despite the cultural and symbolic differences there seemed a great deal of overlap with western magical techniques. Tibetan magic derives from Bon Shamanism overlaid with Buddhist ideas with some input from Hindu thought.
Did magic bring anything to your parenting, and did you learn anything about magic raising kids?
I tried to encourage their imaginations and their ability to visualise. They both got degrees in biological sciences and one carried on and got a PhD, now they teach me a lot about nature and biology. I found it fascinating to watch their consciousnesses and personalities emerge, and how they chose their opinions. Neither of them really got into magic, it did not form part of their cultural milieu or peer group interests which seemed more centred on yoga and meditation and sports.
You say in liber null that white magic leans toward the acquisition of wisdom and a general feeling of faith in the universe, does that not include yoga and meditation? or what parts are missing?
Most forms of yoga and meditation do not include activities designed to make wishes about exterior things come true. However, India seemed overflowing with gurus, sadhus, and ‘holy’ men trying to make a living or a fortune out of peddling questionable spiritual services and practices. A lot of people on mystical and spiritual paths seem to acquire the habit of despising attempts to make things happen by magic and do not even try to make good things happen - basically because they fear they will fail and compromise their faith in their beliefs. Magic does not always work, it often fails, but to me that means just do a lot more of it. If it only works one time in five it still provides a powerful edge if used cunningly.
Do you think magic is for everyone? is this a science that should be taught to school children or is there always going to be a form of shaman in communities?
Well, we now attempt to teach some science to everyone in schools. Perhaps we could introduce elementary magic in disguise by teaching the usefulness of stilling the mind, visualising, and imagining desired intents, exploring the subconscious, developing personified forms of inspiration, and so on. Obviously at this stage in our culture we would have to call it something other than ‘elementary magic’.
Can you say a little bit about how your chaos magic in business class differed from your other work?
We looked at the whole process of setting up a business as a series of magical operations. Illumination to clarify motives and inspirations for the business ideas. Invocation to bring forth the personal qualities to make it happen. Divination to discover relevant information. Enchantment to increase the probability of desired events occurring. Evocation to bring forth staff and allies.
What are your thoughts on Leary and Wilson's theories about the evolution of consciousness and chaos magic sort of being the think edge of that wedge?
The human mind seems the most complicated object we have so far detected in the universe although the entire internet, now approaches the same complexity and information storage capacity as a single human brain, (we just do not have the same memory recall, we have creativity and imagination instead - precisely because of this). Now the human mind has the astonishing capacity to supply some confirmation of almost any scheme we choose to project upon it. Thus, if you attempt to project a Freudian or Jungian or Kabbalistic or Behaviourist or Astrological or Evolutionary Biological or Pagan Polytheist or Monotheist/Dualist scheme on to it, it will provide appropriate feedback or observations that you can interpret within the chosen scheme. All psychology seems more or less arbitrary; but some nonsense proves more useful in some situations than others. I prefer ‘Situational Beliefs’.
Oregon, my home state, just legalized magic mushroom therapy. how do you feel about psychedelics?
I think they have a value in demonstrating what the mind can do, but the magician should then strive to achieve such states by meditation and imagination alone. I have seen too many magicians fall into the trap of using them as a substitute for magic.
Do you think physical aliens have visited earth?
There seems no material evidence, but aliens with the knowledge and power to get here would almost certainly have the ability to remain completely invisible to us and a strong motivation to remain so. If they can move freely around the universe then we have nothing that they could want, except the opportunity to observe us undisturbed, out of curiosity.
What are your hopes for the future?
As a species we urgently need to find an alternative to economies based on debt, and growth in population and consumption. As I said before - This planet cannot even support current levels of human population and consumption in the medium term, let alone in the longer term. Profound or catastrophic changes to the whole human adventure seem inevitable within the lifetime of my children and grandchildren. I hope we take the least bad of the tough options ahead. In general terms we need to focus on quality rather than quantity.
Why is astrology not an ideal divination system?
It all depends on how you define astrology and how you define divination.
Mundane Astrology developed in the ancient world for the purposes of deciding the best times to do things like planting seeds, starting military campaigns, crowning monarchs, breeding, or slaughtering animals, and maybe navigation as well. Heck, we seem to have built the mighty Stonehenge primarily to calculate the exact date in a climate with deceptive weather. The Natal Astrology that developed in the late Hellenic world seems to have almost zero objective predictive power despite that health and life outcomes in temperate climes have a weak correlation to season of birth, but less so as we lead more pampered indoor lives.
On the other hand, the baroque Neo-Platonic inspired nonsense of natal astrology does have a value in Lateral thinking and Apophenic thinking and it can also offer a symbolic alphabet for the construction of spells and rituals. I might also add that it can prove useful in pulling the wool over people’s eyes, manipulating them, and extracting money from them.
Any book recommendations from your current reading list or from your lifelong list of favourites?
I can of course heartily recommend my own six books which may well save the aspiring magician from ploughing through the vast number of classic source tomes from antiquity to Mathers, Spare, and Crowley from which I partly distilled them.
I can also recommend the following for their alternative perspectives on magic: -
My Years of Magical Thinking by Lionel Snell. This explores magical philosophy in depth.
The 7 Laws of Magical Thinking – How irrationality makes us healthy, happy, and sane, by Matthew Hutson. Written by a highly rational man.
Sorcery by J. Finley Hurley. An intriguing investigation into whether magic really works.
Placebo - The belief effect, by Dylan Evans. The astonishing effects of expectation.
Lost in the Cosmos - The last self-help book, By Walker Percy. Quirky and immensely though provoking.
Plus, for entertainment read anything and everything by Sir Terry Pratchett, one of the few novelists who wrote about magic from an insider’s perspective. I guess its okay to mention that now that he has sadly left us.
Winter Solstice 2020
Winter Solstice 2020
Seasonal Greetings.
Astrology. For those who choose to invest belief in it, a rare conjunction of Saturn and Jupiter occurs at this Solstice. This does not necessarily presage the end of the world – fortunately the Chaobala of the Epoch attributes a Saturnine-Jupiterian current to Osiris - the embodiment of rebirth.
Physics. Herewith a seasonal gift to the world: -
https://www.specularium.org/hypersphere-cosmology
After many years of struggle the maths of Hypersphere Cosmology have achieved complete internal coherence and a precise match with observational data. The LCDM Big-Bang Theory will become formally discarded soon, and thank the gods for that, it brought some very distasteful metaphysics with it. Many thanks to all he terrestrial and extra-terrestrial intelligences who have assisted with this project, JD and Yog-Sothoth in particular.
The science media voice increasing doubts about the Big-Bang, the Editor’s Pick letter in the xmas edition of New Scientist begins ‘Time to abandon the big bang theory? Plus, the daft idea of so-called dark matter has just come under further attack from the ‘External Field Effect’ (try searching on that), Hypersphere Cosmology resumes this MOND type effect and identifies and quantifies its origin in Gödelian and Machian principles.
The mathematics off Hypersphere Cosmology condense to a few terse pages accompanied by about forty pages of explanation and metaphysical interpretation. These will appear eventually in the forthcoming Occultaris. In the meantime, the maths appears on this site ‘pour encourager les autres’.
The completion of that part of the Natural Philosophy project opens the way for a serious alternative to the mess of Quantum Field Theory. A gradually emerging model of Quantum Hyperspheres shows promise – in this, everything becomes the cause of itself in hyperspherical space and hyperspherical time. In the best traditions of natural philosophy this leads to an holistic reality in which the properties of anything depend on the whole of the rest of the universe, and many of the strange connections that Apophenia suggests have a reality.
Politics.
Britain seems close to finally liberating itself from the EU Synarchy.
The Eurocrats cannot possibly offer Britain anything less than punitive terms if it refuses to accept political interference, otherwise many other countries will try to regain their political independence and the whole rotten corrupt EU shambles will disintegrate.
Ever since the founding of the Common Market a clique of largely unelected synarchists has promoted a conspiracy to rule Europe through a vast non-democratic bureaucracy that controls every aspect of its citizens lives. It has done this by stealth, by coups, and by bluff.
When Britain conducted a referendum in 1975 on joining the Common Market, strange bedfellows united to oppose the idea. Tony Benn on the far left opined against a ‘Capitalist’s Europe’ and Enoch Powell on the far right said that it would lead to a ‘Progressive Loss of Sovereignty’. The ‘Yes’ campaign made much of the ‘nutters alliance’ opposing the Common Market, yet history has proved both Benn and Powell right. The Common Market mutated into a political project largely beyond democratic scrutiny and it developed the ingenious ruse of putting big business in charge of an ever-expanding regulatory culture that actively supresses competition from smaller businesses. Plus, it became heavily protectionist to shield European big business from outside competition.
Powell also raised controversial early objections to immigration. The burden of immigration falls almost entirely on the indigenous poor by depressing wages and causing housing shortages and increasing crime. The well off reap the benefits in terms of cheap labour and inflating property prices, and even the increased crime and declining social cohesion provides the well off with plenty of administrative opportunities.
Britain will undoubtedly suffer in the short term for a No-Political-Strings-Hard-Brexit but we must do this for the long term benefits: -
Freedom from EU control over our Agriculture and Fisheries which currently degrades the environments of both.
Freedom to control our own borders.
Freedom to decide by democratic means, our own laws.
Freedom to trade with the rest of the world on our own terms.
Freedom always costs. The price, however high, always proves worth paying in the end.
