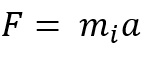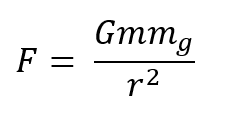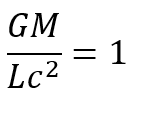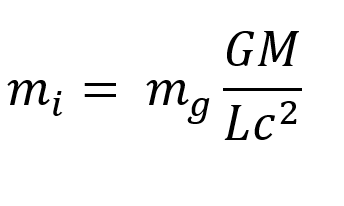Abstract.
This paper presents a quantitative equation for Mach’s Principle that appears to satisfy the requirements of most of the qualitative expressions of Mach’s Principle, and it suggests that the universe has spatial closure and a Transactional gravitational exchange mechanism.
Mach’s Principle.
We recognise mass as having two familiar components, firstly inertial mass – a resistance to acceleration as quantified by Newton’s second law that force equals mass times acceleration, shown here by denoting the mass involved as the inertial mass.
Secondly mass also exhibits a gravitational effect, any two masses appear to attract each other with a force described by Newton’s equation of gravity. In this, the force between a mass m (usually a large mass like a planet or a star) and the mass of interest depends on both masses, the gravitational constant G, and the square of the distance between them. He we denote the mass of interest (which usually means the smaller one that falls or moves most) by its gravitational mass
Now in Newton’s theory, inertial mass miraculously seems to exactly equal gravitational mass and this equivalence explains Galileo’s observation that all masses fall at the same rate. Thus although a heavier mass has more inertia and needs more force to move it, its greater mass gives gravity an exactly proportional extra amount of gravitational mass to work on, so to speak, so all masses fall at the same speed.
On the human scale, inertial mass often seems intuitively ‘stronger’ than gravitational mass, we can feel the resistance a cannon ball offers to our pushing it around, but we cannot feel the gravitational attraction between it and ourselves. This arises because the ‘ratio’ between gravitational mass and inertial mass has a very small value represented by G, the gravitational constant. Nevertheless, the ratio remains constant and an amount of material that has a certain amount of inertia will always have a certain corresponding amount of gravity.
Now Einstein saw something deeper and beyond mere convenient coincidence in the equivalence of inertial and gravitational mass (or more precisely in the equivalence of acceleration and gravity), and he reformulated our ideas about gravity.
He described gravity not as some sort of force at a distance but as an effect arising from the curvature of spacetime by mass. Thus, a massive object like a planet curves spacetime about itself and freely moving objects all follow this curvature by falling towards it at the same rate, and they do not actually feel any forces at all whilst in free fall.
‘Spacetime tells matter how to move; matter tells spacetime how to curve.’ As John Archibald Wheeler so elegantly summarised the idea of General Relativity.
The description of gravity as spacetime curvature gives far more accurate predictions than the basic Newtonian model but it does not say much about the inertial component of mass. In the Newtonian model, inertial mass just appears as somehow intrinsic to an object and gravity appears as a mysterious ‘force at a distance’. Neither of these ideas sits comfortably with the relativistic perspective in which properties arise on a relational basis.
Mach's Principle has hung around on the fringes of cosmology and relativity for 100 years, it has influenced a number of theorists but nobody seems to have managed to formulate it concisely or to develop some maths for it. Roughly speaking it suggests that the inertial mass of any object arises because of the effect of all the stuff in the entire universe, so as Mach put it, if the subway jerks, the far stars and galaxies throw you to the ground
This idea has lurked within physics since Einstein named it after some remarks by Mach (who devised the Mach numbers for multiples of the speed of sound). Nobody appears to have found a way to quantify it and various qualitative versions of it exist. It broadly states that some relationship should exist between the inertia of any body and ALL of the rest of the material in the entire universe. This would seem to imply a spatially closed universe, otherwise inertial mass, and many of the laws of physics, would vary with time.
Debate rages about whether General Relativity really incorporates Mach’s Principle or not. The currently most popular interpretation of cosmological observations asserts that the universe expands from some sort of a big bang, in which case Mach’s Principle seems invalid unless inertial masses either vary with time or remain invariant to the distribution of matter within the universe. As it appears that the distribution of matter in the universe always remains homogenous on a large scale, this distribution invariance comes down to an invariance to the size of the universe which seems highly unlikely as the spacetime curvature we recognise as gravity remains very much distance dependent.
Now if the inertia of any object depends on the entire rest of the universe then it must depend on the gravitational mass of the body in question, the gravitational mass of the entire universe, the Gravitational constant that relates them, and the size of the universe, and the speed of light. Moreover, the ratio of inertial to gravitational mass must remain constant as we have every indication from astronomy that it has not varied over the observable history of the universe.
Now in Hypersphere Cosmology1 , which posits a non-expanding universe: -
Where G = The Gravitational constant
M = The Mass of the universe
L = The antipode distance in a hyperspherical universe
c = The speed of light.
This strongly suggests that the following equation quantitatively fulfils the major qualitative requirements of most expressions of Mach’s Principle.
If the gravitational constant of the universe or the mass of the universe were to increase so would all inertial masses, conversely any increment in the size of the universe or lightspeed would decrease all inertial masses.
GM/Lc^2 thus appears as a sort of scalar field, omnipresent and apparently non-local* in the hypersphere of the universe, and giving rise to an acceleration A = GM/L^2 which has detectable effects such as the Pioneer anomaly and the anomalous galactic rotation curves.
(See Hypersphere Cosmology1 )
At present the equation has no practical use except to complete hypersphere cosmology because there seems no way we could currently manipulate the effects of G,M,L, or c, in the vicinity of a spacecraft, but if we could reduce inertial mass somehow then we could easily move matter around the universe.
*The apparently instantaneous effects of both inertia and ‘static’ gravitational spacetime curvatures raises interesting questions. Gravitational waves undoubtedly propagate at light-speed from accelerated masses as Einstein predicted and as recent experiment has confirmed.
If we accept that nothing can travel faster than light then the apparently instantaneous effects of inertia and static spacetime curvatures, (gravity ‘fields’) may arise from a Transactional Exchange between curvatures. The laws of gravity seem completely time symmetric and capable of supporting advanced negative curvatures propagating down retarded positive curvature paths back into the past to create apparently instantaneous effects.
The time-symmetric nature of all physical laws except the Second Law of Thermodynamics (which states that in an isolated system Entropy will increase only) at first appears very mysterious and physicists usually quietly ignore the time reversed solutions to their equations and calculations.
Hawkin remarked that ‘Entropy increases with Time because we measure Time in the direction in which Entropy increases’. We have no way of telling in which ‘direction’ ‘time goes’ or even if it actually ‘goes’ anywhere.
If however, we adopt the Transactional Interpretation and extend it beyond quantum physics to gravitation and to model gravitational effects as arising from positive spacetime curvatures propagating forward in time and negative spatial curvatures propagating backwards from the future to create effects in the present then we can explain the apparently instantaneous effects of inertia and static gravitational ‘fields’.
Of course, the same argument applies to electrostatic fields that would then correspond to a special class of spacetime curvatures.
Accelerations of masses and electrostatic charges will of course create disturbances in spacetime curvatures that propagate at light speed as bosons with the wave –particle duality characteristic of quanta. However, the concept of virtual bosons mediating static gravitational and electrostatic interactions becomes redundant.
Reference1.
Hypersphere Cosmology 2. Author: Peter J Carroll. http://vixra.org/abs/1601.0026